Cosine Rule

$GCSE Maths Revision$

Note – The Cosine Rule is considered a higher topic on most exam boards.

$GCSE Mathematics Revision - Area of a Triangle using Sine$

Another trigonometric formula for any type of triangle is the Cosine Rule:

$c^2 = a^2 + b^2 - 2ab\cos{C}$

or alternatively

$a^2 = b^2 + c^2 - 2bc\cos{A}$

or

$b^2 = a^2 + c^2 - 2ac\cos{B}$

Where the uppercase letters correspond to the angle, and the lower case letter is the side opposite it.

The different formulas are provided for use depending on what sides/angles you are given. I recommend choosing just one, learning that and changing the sides/angles accordingly.

The Cosine Rule is used when you have either two sides and an angle or three sides.

Did you know? – In France, the Cosine Rule is called Théorème d’Al-Kashi (Theorem of Al-Kashi) after the Persian mathematician Jamshīd al-Kāshī, who was one of the first to provide a formula of the rule.

Example 1

$GCSE Mathematics Revision - Finding an angle using the Cosine Rule$

Find the angle A in the above diagram.

The angle we are dealing with is A, so using the formula;

$a^2 = b^2 + c^2 - 2bc\cos{A}$ ,

we get:

$9^2 = 10^2 + 11^2 - 2(10)(11)\cos{A}$ .

Rearranging this results in:

$220\cos{A} = 140$ , so $\cos{A} = \frac{140}{220} = \frac{7}{11}$ .

So, using the Inverse Cosine Function, we get:

$A = cos^{-1}{\frac{7}{11}} = 50.48$ to 2dp.

Example 2

$GCSE Mathematics Revision - Finding the length of a side using the Cosine Rule$

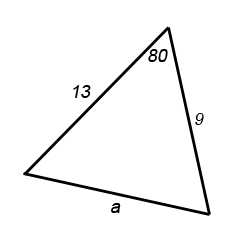
Again using $a^2 = b^2 + c^2 - 2bc\cos{A}$ ,

we get:

$a^2 = 13^2 + 9^2 - 2(9)(13)\cos{80}$ .

This gives $a^2 = 209.366$ .

Taking the square root gives us the length of a as $a = \sqrt{209.366} = 14.47$ .

It’s important to remember that the questions you may be asked in an exam might not be quite as obvious to answer as these examples. Often it is up to you to understand and interpret what the question in asking you. Remember, before trying to answer any question of this sort, DRAW A DIAGRAM!

Cosine Rule

Share this Page

Blogroll