Note – The Sine rule is considered a higher topic on most exam boards.

As well as the usual trigonometric formulas for right angled triangles, there’s also a handy little formula that you can use for any triangle. This is known as the Sine Rule and can be used to find the size of the angles or the lengths of a side. The formula is as follows:
or alternatively
Where the uppercase letters correspond to the angle, and the lower case letter is the side opposite it. It doesn’t matter which one you use, but I recommend the first one if you’re working out an angle, and the second one if you’re working out the length of a side. This is just to simplify your calculations.
The Sine Rule can be used when you have either two sides with an angle opposite to one of the sides or one side and any two angles.
Example 1
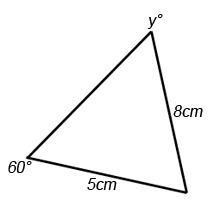
Find the angle y in the above diagram,
Using the first of the formulas above, we get .
Rearranging gives .
We then use the inverse sine to get to 2dp.
Example 2
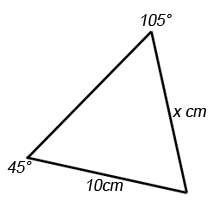
Find the length x in the above diagram.
This time we are going to be using the second of the above formulas. Subbing in the above values we get .
Rearranging gives to 2dp.
You have now seen how to find both sides and angles using the sine rule.
See also the Cosine Rule


