Sine, Cosine & Tangent

Trigonometry is the mathematical study of triangles and the relationships between their sides and angles. It’s an extremely useful branch of mathematics which has a wide range of uses, from navigation to controlling the robotic arm on the International Space Station.

Trigonometry gets it’s name from the Greek Trigōnon Metron (Triangle Measure).

Sin, Cos & Tan

$GCSE Mathematics Revision - Sin Cos Tan Triangle$

A right-angled triangle, obviously enough, is one which contains a right angle. Before we can go on we now need to give a name to the sides of the triangle. The hypotenuse is the diagonal, opposite the right angle. The adjacent side is the other one forming the angle, while the opposite side is the one opposite our angle.

For any angle $x$ in a right angled triangle:

Sine (sin) $x$ = $\frac{\mathrm{Opposite}}{\mathrm{Hypotenuse}}$

Cosine (cos) $x$ = $\frac{\mathrm{Adjacent}}{\mathrm{Hypotenuse}}$

Tangent (tan) $x$ = $\frac{\mathrm{Opposite}}{\mathrm{Adjacent}}$

It may help to write it as $\sin = \frac{o}{h}$ , $\cos = \frac{a}{h}$ and $\tan = \frac{o}{a}$ , and many people memorise the word SOHCAHTOA.

Example 1 – Find the length of the side labelled h in the diagram below.

$GCSE Mathematics Revision - Trigonometry Example, Sin Cos Tan$

The two sides involved in this calculation are the opposite and adjacent, so looking at the formula we have above, we are going to be using the tan formula:

$\tan{x} = \frac{\mathrm{Opposite}}{\mathrm{Adjacent}}$

So putting in our values above, $\tan{30} = \frac{\mathrm{h}}{25}$ , so rearranging this we get $\mathrm{h} = 25(\tan{30})$

Using our calculator, we get $\mathrm{h} = 25(0.577350) = 14.433757$

So the length of our side, to two decimal places is 14.43m.

Example 2 – Find the angle labelled x in the diagram below.

$GCSE Mathematics Revision - Trigonometry Example, Sin Cos Tan$

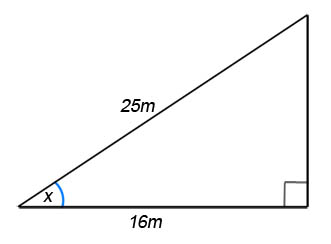
Again to start this off we need to look at the two sides involved, this time it’s the adjacent and the hypotenuse, so either by looking at the above formula, or remembering SOHCAHTOA, we know what we’re going to be dealing with the cos function, namely:

$\cos{x}$ = $\frac{\mathrm{Adjacent}}{\mathrm{Hypotenuse}}$

Putting in our values from our triangle, $\cos{x} = \frac{16}{25}$ , but where do we go from here?

It’s now time to pull out the calculator once more. The function we will be using is the inverse cos function. This is often written $\cos{}^{-1}$ , (see diagram below for more). This basically reverses the cos function.

Looking back at our question, we have $\cos{x} = \frac{16}{25}$ .

Inverse cos of $\cos{x}$ is just $x$ , and using our calculator, inverse cos of $\frac{16}{25}$ is $50.208181$ . So our angle, to 2 decimal places, is $50.21^{\circ}$

You may sometimes need to use Pythagoras’ Theorem to find the lengths of certain sides.

See here for more on Inverse Trigonometric Functions.

In addition, there are also two trigonometric rules used on the Higher papers, these are the Sine Rule and the Cosine Rule.

Graphs of Sin, Cos & Tan

Sin

$GCSE Mathematics Revision - Sin Graph$

The above is the graph for the Sine Function. From this graph we can tell that Sin is a bounded function, the greatest value it can take is 1, and least -1. You can check this yourself on your calculator. Sin is also a periodic function, meaning that it repeats itself every set period, for Sin this is every 360°. For any angle $\theta$ , $\sin{(\theta)} = \sin{(\theta + 360)}$

You can also tell by looking at the graph that $\sin{x} = 0$ when $x = 0, 180, 360$ …

Cos

$GCSE Mathematics Revision - Cos Graph$

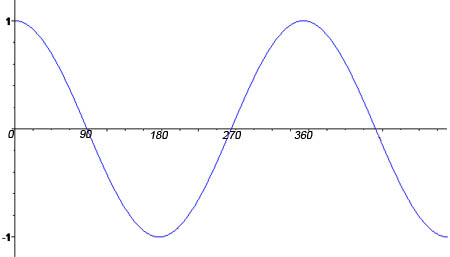
You will see that the graph of the Cosine function is very similar to the Sin function. In fact it’s actually the Sin graph, shifted to the right by 90°. As with Sin, the Cos function is also bounded by 1 and -1, and similarly has a period of 360°. Because of this, for any angle $\theta$ , $\cos{(\theta)} = \cos{(\theta + 360)}$ .

Looking at the graph you’ll be able to see that $\cos{x} = 0$ when $x = 90, 270,$ … Another thing you can see from the graph is that Cos is symmetrical about the y axis. Because of this you can use the fact that $\cos{(x)} = \cos{(-x)}$

Tan

$GCSE Mathematics Revision - Tan Graph$

The Tangent graph you may notice, at first seems nothing like the graphs of the other two, nevertheless it does have certain similar properties.

Tan is periodic with a shorter period of 180°. It is not however, bounded. You will notice that as the functions approaches 90, 270… it “shoots off” to infinity. The red lines of the graph are called asymptotes, these are not actually part of the graph, they are there to show that the Tan function is never actually equal to these numbers, it just gets infinitely close.

For a more in depth look at the graphs of trigonometrical functions, be sure to have a look at our article on Trigonometric Graphs.

Did you know? – This is not needed for your exam, but some of you may be interested to know that $\tan{x} = \frac{\sin{x}}{\cos{x}}$ . This explains why Tan is equal to zero when Sin is, and why Tan doesn’t exist for when Cos is equal to zero, because you all know that you can’t divide by zero right?

"Sine, Cosine & Tangent" is part of the Trigonometry section.