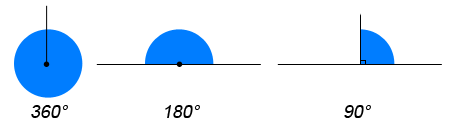
Angles are used to measure rotation around a fixed point. They are measured in degrees, written with the degree sign °. The maximum angle is a full rotation which is 360°, (shown below). Half of this angle is 180°, which is the angle on a straight line.
Another common angle is 90°, this is a quarter turn of a circle and is indicated by a small square in the corner of the angle. This is more commonly known as a right angle.
Did you know? – The word angle comes from the Latin word angulus, meaning a corner.
Types of Angles
There are generally 4 types of angles you will encounter in your Maths GCSE, shown below.
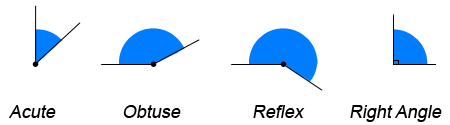
Acute Angle – An Acute angle is any angle less than 90°.
Obtuse – An Obtuse angle is an angle greater than 90° but less than 180°.
Reflex – A Reflex angle greater than 180° but less than 360°.
Right Angle – A Right Angle, as we saw above, is an angle of exactly 90°.
Related Angles

The lines WX and YZ are parallel to one another, (indicated by the >> on the lines).
Alternate angles – Angles d and f are alternate angles. These angles are equal to each other. These angles often form a Z shape and are often known as “Z Angles”. (Angles c,e are also alternate.)
Corresponding angles – Angles a and e are corresponding angles. When two parallel lines are crossed by another straight line, (called the transversal), the angles in the matching corners are known as corresponding angles. (Angles b,f, d,h, c,g etc. are also corresponding.)
Interior angles – Angles d and e are interior angles. These two angles add up to 180°. (Angles c,f are also interior.)
Supplementary Adjacent angles – Angles a and b are supplementary adjacent angles. Supplementary angles add up to 180° and Adjacent angles are ones that share a common line or corner. Therefore supplementary adjacent angles are angles on a straight line which add up to 180°. (Angles b,c, c,d, d,a etc. are also supplementary.)
Vertically Opposite angles – Angles a and c are vertically opposite angles, these are equal to each other. (Angles b,d, e,g and f,h are also vertically opposite.)
Interior Angles of a Triangle
An extremely useful fact in Geometry is that the interior angles of a triangle add up to 180°. Using a couple of the angle facts above we can easily prove this.
For any size or shape triangle ABC with angles x, y, z let’s draw a pair of parallel lines above and below it, shown below.

As these two lines are parallel, we can use the Alternate (or Z angle) fact to label the two more angles y and z as below.

We know that the angle on a straight line on a straight line is 180°, so we can say that x + y + z = 180°. Therefore the interior angles of a triangle add up to 180°.
Interior Angles of a Quadrilateral
We’ve dealt with the interior angles of a triangle, now for the interior angles of any quadrilateral (4 sided shape).
If you look at the diagram below, you will see that we can divide any quadrilateral into two triangles.

Applying what we learn above, the sum of the interior angles of a quadrilateral is the same as the sum of two triangles. 180° + 180° = 360°. Therefore the sum of the interior angles of any quadrilateral is 360°.
Exterior Angles
The exterior angles of a shape are the angles you get when you extend the sides. The exterior angles of a square are shown below.

As you can see the sum of the exterior angles of a square is 360°. This fact actually applies for any regular polygon, (a polygon where all the sides and angles are the same), the exterior angles add up to 360°.
In the square for example, the exterior angles is 360° divided by the number of sides, = 90°.
Interior Angles of a Regular Polygon

In the picture above, the blue angle is the exterior angle we worked out before, and the red angle is the interior angle.
One you have worked out the exterior angle, the interior is very easy to calculate using the following formula:
Exterior Angle + Interior Angle = 180°
So in the case above, the Interior angle of a square would be 180° – 90° = 90°.


